Description:
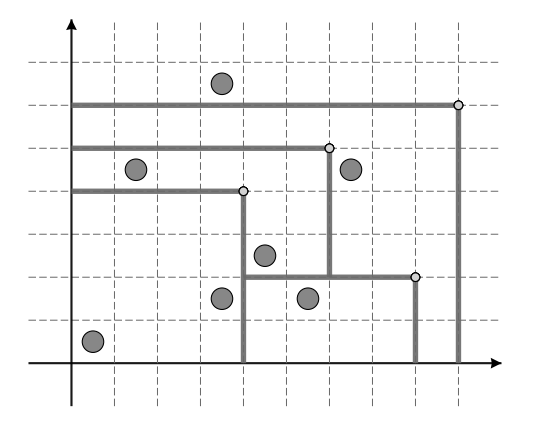
在一个网格平面上,有\(n\)个点(牛),其中第\(i\)个点在以\((x_i,y_i)\)为右上角的网格中。有\(m\)次操作,每次给出一个点\((x,y)\)(栅栏),表示从\((x,y)\)开始,向左和向下画线直到与之前画的线或坐标轴相交。这样会划分出以\((x,y)\)为右上角的新区域。你需要对每次操作求出,新区域中点的数量。
\(n,m\leq 3 \times 10^5, 1 \leq x_i,y_i \leq 10^9\)
Example:
| input | output |
| 7 1 1 4 2 6 2 5 3 2 5 4 7 7 5 4 4 4 8 2 9 6 6 5 | 2 1 3 2 |
Solution:
1.首先用扫描线+set处理出最终状态下的每个栅栏控制的点的数量。
即求每个牛被哪个栅栏控制。
将所有点(牛和栅栏)按\(y\)坐标递减排序后依次处理每个点。
用set维护当前状态下,所有点组成的栅栏向下延伸将\(x\)坐标分成了几个部分。要处理其中有些栅栏向下延伸的边会被\(y\)坐标比它小但出现时间比他早的栅栏向左延伸的边切掉。
考虑加入一个栅栏点。则模拟向左延伸并删除之前出现(\(y\)坐标比它大)\(x\)坐标比他小,出现时间比他晚的栅栏。直到遇到第一个出现比它早的栅栏,此时该栅栏向左延伸的边被阻断。
考虑统计每个点(牛)最终属于哪个栅栏。当处理到一个点(牛)时,此时\(x\)坐标被之前出现的栅栏分割成了几个部分,显然,该点最终会属于第一个比它的\(x\)坐标大的竖线所代表的栅栏。
2.然后考虑栅栏之间的影响。
任意两个栅栏A,B之间只有三种情况。
1.A,B不构成包含关系:A,B的答案互不影响。
2.A包含B,但A出现的时间比B晚:B的答案不需要被算入A的答案。
3.A包含B,且A出现的时间比B早:B的答案需要被算入A的答案。
因此,只需处理出包含关系构成的森林(每个栅栏向与它最靠近的在它右上的栅栏连边,该过程可以在维护set的时候顺便完成),然后按照时间顺序依次处理每个栅栏,每个栅栏的最终答案就是当前子树的size,然后将它的父边删去。
然而这么搞不好写(lct滚呐),可以按时间倒序处理,(考虑先每个点孤立,不停加边)用并查集维护答案。
Code:
#include <set>
#include <cstdio>
#include <algorithm>
#define fi first
#define se second
#define mp make_pair
#define FOR(a,b,c) for(int a=b;a<=c;a++)
#define FORD(a,b,c) for(int a=b;a>=c;a--)
using namespace std;
typedef pair<int, int> pii;
struct pt {
int x, y, t;
}a[600010];
int cmp(pt x, pt y) {
if (x.y == y.y) return x.t > y.t;
return x.y > y.y;
}
int n, m, x, y, cnt;
set<pii> s;
int fa[300010], num[300010];
int f[300010];
int ans[300010];
int find(int x) {
if (f[x] == 0) return x;
return f[x] = find(f[x]);
}
int main() {
scanf("%d", &n);
FOR(i, 1, n) {
scanf("%d%d", &x, &y);
a[++cnt] = {x, y, 0};
}
scanf("%d", &m);
FOR(i, 1, m) {
scanf("%d%d", &x, &y);
a[++cnt] = {x, y, i};
}
sort(a + 1, a + cnt + 1, cmp);
FOR(i, 1, cnt) {
if (a[i].t) {
pii tmp = mp(a[i].x, a[i].t);
s.insert(tmp);
set<pii>::iterator now = s.find(tmp);
if (++now != s.end()) fa[tmp.se] = now->se;
now = s.find(tmp);
while (now != s.begin() && (--now)->se > tmp.se) {
s.erase(now);
now = s.find(tmp);
}
}
else {
set<pii>::iterator now = s.lower_bound(mp(a[i].x, 0));
if (now != s.end()) num[now->se]++;
}
}
FORD(i, m, 1) {
ans[i] = num[find(i)];
if (fa[i]) {
x = find(i), y = find(fa[i]);
f[x] = y;
num[y] += num[x];
}
}
FOR(i, 1, m) printf("%d\n", ans[i]);
return 0;
}